ECE243

Spring 2005

Andreas Moshovos

Subroutines – Examples

We will look at two subroutine examples. We may not cover both of them during the lectures. You may use those that we do not cover as practice questions. That is, try to develop code for the C equivalents and then compare your solution to the ones presented here.

1. Searching Through a Sorted Binary Tree

A binary tree is a data structure comprising several nodes. Each node has three components:

      1. A data value

      2. A left child

      3. A right child

Both children are also nodes. In C we can define a tree using the following structure:

struct node_t

{

int   value;

struct node_t *left;

struct node_t *right;

}

A binary tree is sorted if the following two conditions apply at each node:

      1. The values of all nodes in the left subtree of a node are less than the value of the node.

2. The values of all nodes in the right subtree of a node are greater than or equal to the value of the node.

The following figure shows a sorted binary tree:

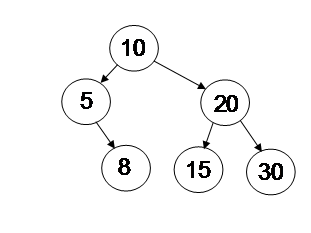
The following C function searches a sorted binary tree for a given value. It returns 1 if the value is found otherwise it returns 0:

int

st_search (struct node_t *tree, int value)

{

struct node_t   *curr = tree;

while (curr)

{

if (curr->value == value) return 1; // value found

if (value < curr->value)            // if value less than that of the current node search the left

curr = curr->left;            // subtree

else curr = curr->right;           // search the right subtree

}

return 0;

}

This routine uses the curr pointer to start searching from the top node following the left or right child pointers until either the value is found or there are no more nodes to search. The following figure shows the path the function will follow if called to search for value 13.

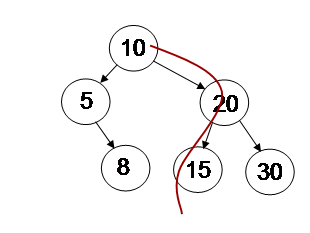
At the machine level the tree has to be represented in memory. Following the “struct” definition in C, each node is represented using three consecutive words in memory. The order and use of the words follows exactly that of the “struct” definition: The first holds the data value, the second word contains a pointer to the left child while the third word contains a pointer to the right child. A pointer has a value which can be used as an address to refer to some other object in memory. Here’s a series of assembler directives that form our example tree:

.equ NULL, 0 # define NULL to be a pointer to address 0. By default this is the NULL pointer in C

# This is a compromise as this way we cannot store an object at address 0 and take its pointer

# but then, there are 2^32-1 other addresses we can use

.data

node0: .word  10, node1, node2  # top node

node1: .word  5, NULL, node3    # top node’s left child

node2: .word  20, node4, node5  # top node’s right child

node3: .word  8, NULL, NULL    

node4: .word  15, NULL, NULL

node5: .word  30, NULL, NULL

Note that the exact order in which the nodes appear in memory is *not* important. That is the following statements define the same tree (when viewed in the abstract) but with a different in memory layout:

.equ NULL, 0

.data

node2: .word  20, node4, node5  # top node’s right child

node3: .word  8, NULL, NULL    

node4: .word  15, NULL, NULL

node5: .word  30, NULL, NULL

node0: .word  10, node1, node2  # top node

node1: .word  5, NULL, node3    # top node’s left child

The next important step is to figure out what the stack layout should be for a correct implementation of st_search. This subroutine takes two arguments: a pointer and a value. So, we do not need to pass any values through the stack.

With this in hand now we can start writing the subroutine.

A concern any time we start developing a subroutine is that often we cannot tell immediately how many registers and local variables (allocated on the stack) we will need. This is important to know as we will have to save registers on the stack prior to using them and since we will have to allocate local variables on the stack. The net effect will be that the relative distance from the stack pointer of the parameters may change. A methodology that would work is to write the subroutine using names for the various parameters and locals and once the subroutine is complete to rewrite saving/restoring any registers we used and replacing parameter names with appropriate displacements from the top of the stack.

Here’s the first implementation that ignores saving/restoring registers:

.text

# r4 contains “tree”, we’ll re-use it for curr

# this OK since the value of r4 does not need to be preserved

# r5 contains “value”

st_search:              

# nothing is needed for curr = tree, we reuse r4

loop:

beq r0, r4, notfound # if reached a NULL pointer

ldw r8, 0(r4) # read curr->value into r8

beq r8, r5, found # if curr->value == value goto found

blt r5, r8, goleft # if the value we are looking for is greater than the one we just read we

# must visit the left subtree

goright:

ldw r4, 8(r4) # curr = curr->right

br loop

goleft: ldw r4, 4(r4) # curr = curr->left

br loop

found: addi r2, r0, 1

br epilogue

notfound:

add r2, r0, r0

epilogue:

ret

In this case no further changes are needed since we did not modify any callee-saved registers and we did not use any stack allocated locals.

SECOND EXAMPLE: Detecting whether a string is a palindrome (or carcinic)

A series of letters is a palindrome if it reads exactly the same if read from left to right or from right to left. For example “abba” is a palindrome and so is “lalal”. “lala” is not a palindrome.

We want to write a function that returns 1 if its string parameter is a palindrome. The function should return a 0 otherwise. Before we do so, let’s first explain what is a string. A string at the machine level is a sequence of bytes. The C implementation of strings uses a zero-terminated sequence of bytes. That is, the end of the string is marked by a byte whose value is zero. This zero is not part of the string, it only marks its end. Hence we cannot have a string that contains the 0 byte. So, “abba” will be represented as five bytes with values: ‘a’, ‘b’, ‘b’, ‘a’ and 0, where for example ‘a’ is the ASCII code for the character a. So, if in C we write:

char s[] = “abba”;

In assembly we would write:

.data

s: .byte      ‘a’, ‘b’, ‘b’, ‘a’, 0 # we are using single quotes. If you copy-paste from this text replace all quote with single quotes.

So, a string is really an unidimensional array. So, using just “s” we are effectively referring to the address of its first element (same as &s[0]).

Alternatively we can write:

.data

s: .string “abba” # We are using double-quotes. If you copy-paste convert all to double-quotes.

This is exactly equivalent. It does allocate the terminating zero.

The function palindrome will have the following interface:

int

palindrome (char *a)

{

}

Hence “a” will be a word whose value is the address where the string starts at.

Here’s an implementation of palindrome in C:

int

palindrome (char *a)

{

char *e;

if (a == NULL) return 1;    // NULL string is a palindrome (we define this)

e = a;

while (*e != 0) e++;              // find the terminating zero

if (e == a) return 1;       // empty string (just a terminating zero) is a palindrome

e--;                        // point to the last character

while ((*a != 0) && (*a == *e))

{

a++;

e--;

}

if (*a == 0) return 1;      // is a palindrome

return 0;

}

Here’s the implementation where we initially ignore saving/restoring registers and the actual distance of parameters from the top of the stack:

.text

palindrome:

beq r4, r0, ret1

add r8, r4, r0 # a is in r4, e = a à r8 = r4

# while (*e != 0) e++

findzero:

ldb r9, 0(r8) # read *e and check if zero

beq r9, r0, foundzero

addi r8, r8, 1 # *e non-zero move to the next byte

br findzero

foundzero:

beq r8, r4, ret1 # if (e == a) return 1

subi r8, r8, 1 # e = e -1

cmploop:

ldb r9, 0(r8) # if not *a != 0 exit the loop

beq r9, r0, after

ldb r10, 0(r4) # if not *a == *e exit the loop

bne r9, r10, after

addi r4, r4, 1 # a++

subi r8, r8, 1 # e—

br cmploop

after:

ldb r9, 0(r4) # if (*a == 0) return 1

beq r9, r0, ret1

ret0:

add r2, r0, r0 # not found return 0

br epilogue

ret1:

addi r2, r0, 1 # found return 1

epilogue:

ret

This is not the best possible palindrome implementation. Our goal is to show one that works and focus on the assembly implementation.

Here’s a main function that calls palindrome with s as the argument:

.text

.globl main

main:

movia r4, s

call palindrome