University of Toronto
Department of Electrical and Computer Engineering
 
ECE241F: Digital Systems
 
Hardware Lab #2 - Counters, Oscillators and Gate Delay

P. Chow and J. Rose

Fall 1996

The purpose of the lab is to understand operation of flip-flops, counters and ring oscillators. You will uses the different parts of this lab to make an actual measurement of the propagation delay of a basic logic gate.

Each of the following sections gets you to build a part of a rather large circuit that you will use at the end to measure the delay of a basic logic gate.

PART I: Ripple Counter and Counting to a Specified Value

1. Build a 3-bit ripple counter with an asynchronous reset (clear) input, as shown in Figure 1. Use the 74LS107 JK flip-flop, a negative edge triggered JK flip-flop, as described in the data sheets handed out in lab #1. The counter outputs are determined by the Q outputs of the flip-flops.

    
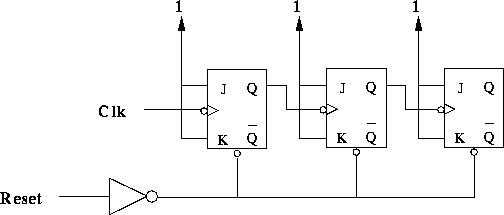
   Figure 1: A 3-bit ripple counter.
   

   Notice that after the Reset signal goes low, the counter is enabled and begins to count. It is often useful to have counters that count up to a specific value and then stop. Design a modification of this counter circuit such that the counter stops counting when it reaches the value 4. (In another part of this lab, we will ask you to make a counter that stops at a different number, so try to come up with a scheme for doing this which you can apply to any stop-count number) The counter should stay at this value until the counter is Reset again. Note the following:

   1. that the 3-bit counter counts from 0 to 7.
   2. do not modify the clock signals going into the flip-flops, just the signals going into the J and K inputs. In general, it is bad design practice to generate clocks with gate logic.

   Build and test this circuit, first by clocking it manually. Then connect it to the oscillator provided in your laboratory setup.

   Note: When building this circuit, you will have some unused inputs. What can happen if you leave them floating (unconnected)? What is the solution?

   Preparation: Enter and Simulate your N=4 counter circuit using LogicWorks. Bring the schematic and simulation printouts. Answer the above question.

2. Design a circuit that generates one positive pulse every time a switch is activated, as illustrated in Figure 2. The pulse width should be equal to the width of one clock cycle, as shown in Figure 2. You should use a modification of the circuit of Part 1, by choosing a suitable value for stop-count value, to obtain the desired pulse.

   Build this circuit. Do not disassemble this circuit. You will need it for PART II.

   Preparation: Enter and Simulate your circuit.

 
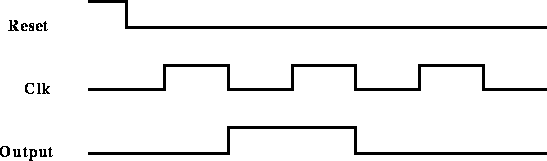
Figure 2: Timing of the desired output.

PART II: Ring Oscillator and Measuring Gate Delay

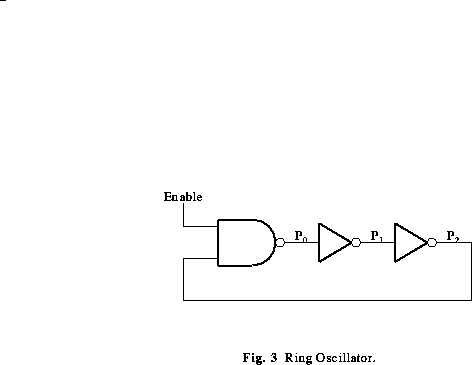
Review of Ring Oscillators

In an earlier lecture we discussed the operation of a Ring Oscillator, as illustrated in Figure 3. The following discussion reviews the operation of that circuit.

The circuit shown consists of three inverting gates connected in a ring. While the Enable input is equal to 0, points 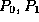, and 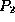will be at logic levels 1, 0 and 1, respectively. Consider what happens when Enable is changed from 0 to 1. The state at point 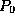is given by:

=

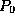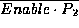
Because of the propagation delay through the gate, the state of 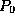at time t is actually a function of the state of the gate inputs at time 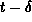, where 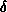is the propagation delay through the gate. That is:

=

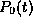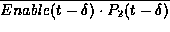
Hence, after one gate delay from the moment Enable becomes equal to 1, 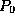becomes equal to 0. One gate delay later, 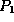changes to 1, and so on. Let 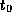be the instant at which Enable changes from 0 to 1. The sequence of events may be described as follows:

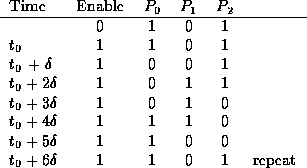
This sequence of events will repeat indefinitely, producing oscillatory signals at 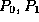, and .

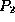1. Draw a timing diagram showing all four signals in Figure 3, starting slightly before ;
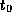2. What is the frequency of oscillation of this circuit?
3. Consider a loop consisting of n gates. Give an expression for the frequency of oscillation as a function of 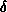and n;
4. What happens when Enable changes back to 0?

Lab Exercise

The purpose of this part of the lab is to use the ring oscillator to measure the gate propagation delay, 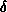, by measuring the oscillator's frequency. Design and build a circuit, given in block diagram in Figure 4, to do so as follows:

• Set Enable to 1 for a known period of time (using the circuit of Part II);
• Count the number of pulses that the oscillator produces during that period.

The required measurements are easily done with the equipment available in the laboratory if you choose the number of gates in the ring, n = 13 and a time period equal to one cycle of the built-in oscillator of your digital board setup. Use two 4-bit counter chips (74LS193) to build an 8-bit counter to count the number of pulses. A block diagram for the required circuit is shown in Figure 4 for n = 5.

Using LogicWorks, first simulate your circuit. The 74193 is available in the 7400 library. It will help you make sure that you have made the correct connections to the chips. You will have to set the delay of the gates in the ring to some value other than the default 1.

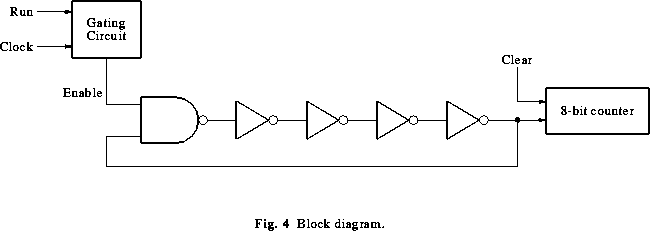
You will use the the built-in oscillator in the digital lab board to provide the input clock. The last page of the handout for lab #1 tells you how to calculate the period of the clock as a function of the capacitor attached to its terminals. When a 10pF timing capacitor is used, it has a period of about 20-25 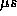but the frequency of oscillation may vary from board to board. You must also take into account about 20pF of parasitic capacitance when using the timing period formula given in the handout. The parasitic capacitance is due to effects such as the protoboard connections and the wires. This will vary from board to board.

Using this set up, measure the propagation delay of the inverters. Do your measurement several times and average the results. Why is this a good practice?

Change your circuit by adding a few more inverters, and redo the measurements.

Preparation: Answer questions 1 to 4 above. Enter and simulate a circuit to do the gate delay measurement, as described above.