Lecture 23
Andreas Moshovos
ďSpringĒ 2005
Building larger memories
using smaller ones
During the lectures we have discussed how memories are organized internally (please read through chapter 5). In this lecture we will explain how we can use smaller memory devices to build larger ones. For example, what if we want to have 4Gbytes of main memory in our system? Turns out that we do not necessarily need to find a 4Gbyte memory chip (I donít think that one exists today anyhow). Instead, what we can do is get a lot of smaller memory devices (say eight 512Mbyte devices) and organize them in a way that they behave like the larger chip would.
Capacity and
Geometry (internal and external)
Before we proceed with the methodology letís first take a closer look at the relevant attributes of a memory device. There are two interrelated attributes:
(1) Capacity and (2) Geometry.
Capacity = total amount of information (bits) that the memory device can store. Example: 16Kbits or 2Kbytes (these two are the same).
Geometry = how information is organized (this is the external view of memory). A memory device has two dimensions: rows and columns:
|
|
<--- columns ---> |
|
|
^ | | rows | | V |
|
Geometry and capacity are directly related: capacity = rows x cols.
As an example, consider a memory device that has a capacity of 32Kbits and is organized in 8K rows where each row contains 4 bits. Often the name ď8K x 4bitĒ will be used to refer to such a device. It is important to note that the geometry of 8K rows and 4 bits per row refers to the external interface of the device. Internally, the memory will be as rectangular as possible to minimize latency. The external interface is different as the goal there is to minimize the number of external connections (pins). For example, a 1Mbit memory device could be organized internally as an array of 1K rows where each row has 1K bits. If we were to expose this organization externally we would need 10 address bits (for the row) plus 1K bits for the data bits of each row. Thatís a lot of pins and while one could probably build a package that has 1000+ pins, the package will be very expensive (and definitely much more expensive than the memory device it will hold).
The externally exposed geometry of a memory device determines the number of address and data lines required. For example, a 8Kbyte chip organized externally as 4K rows of 16 bits each has the following wires:
A12-A0 : row address
D15-D0 : data lines
R/W : whether we want to read or write
E: whether we want to access this device
If E = 0 the device sits silent and ignores all other signals. If E = 1 then it looks at R/W and if it is 1 it does a read or a write. In either case the address accessed must be given on the address lines.
External Data
Connections: Why we can share them across multiple memory devices
The connection for the data lines is similar to the connection used for the external connections of the PIT:
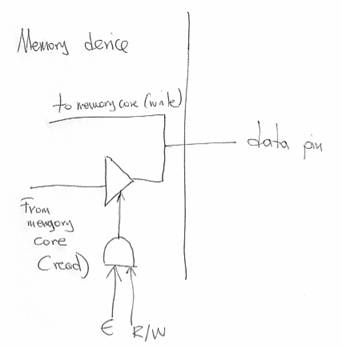
There is a tri-state buffer and a direct connection to the external data pin. If we are reading from the device (E AND R/W) then the tri-state buffer is enabled and the value read from the internal memory array is placed on the data pin. If we are not reading from the device, then the tri-state buffer is de-activated and the data pin is left floating. For writes, the internal memory core has a direct connection so that it can use the value placed there by someone else (typically the CPU). This arrangement allow us to connect multiple memory devices onto the same data pins. So long as we make sure that only one of them is driving the data line (i.e., we read from only one device) there is no short-circuit and everything works fine.
Synthesizing a
Wider Memory using Narrower Ones: Having More Columns
As we have seen a memory device has two dimensions: rows and columns. Letís first see how using smaller devices (narrower) we can synthesize a wider one. That is, letís see how we can increase the column dimension. This is best understood by means of an example. Assume that we are given memory devices that are 8Kbits (capacity) organized as 2K rows of 4 bits each. What we want to have is a memory device of 16Kbits capacity organized as 2K rows of 8 bits per row.
HAVE: 2K rows x 4 bits/row
WANT: 2K rows x 8 bits/row
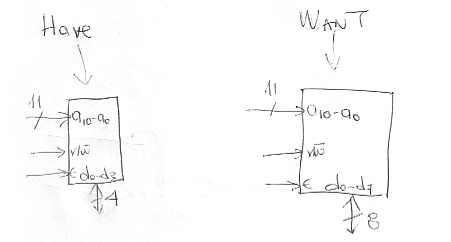
One of the things we need to determine is how many of the smaller devices we need to build the larger one. We could look at the capacity. The smaller ones are 8Kbits each and the one we want is 16Kbits. So, if we consider only capacity two of the smaller chips should be sufficient (in our example, we will be using 100% of all memory devices, however, as we will explain later it may be necessary to only partially use some of the smaller chips depending on the geometry of the ďwantĒ device).
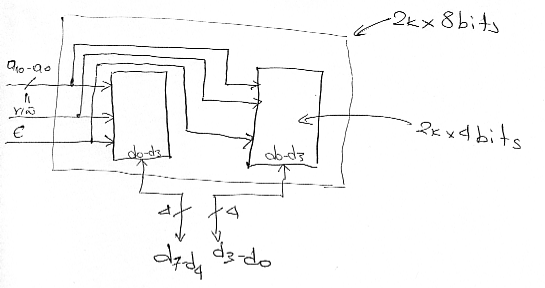
Having two of the smaller devices we must now connect them so that they collectively behave like the larger device. The idea here is to place the two small devices conceptually next to each other, access the same row in both devices and use the four bits from one of the devices as the four most significant bits of the output and the four bits from the second device and the lower four least significant bits of the output. The connections are as follows:
 †
†
The 11 address lines are connected to both devices. The four bits of one of the devices are used as the upper four data bits whereas the four bits of the second device are used as the four lower data bits. The E and R/W signals are connected to both devices because at every access we do access both devices in parallel performing the same type of access.
Synthesizing a
Taller Memory using Shorter Ones: Having More Rows
Letís us now use smaller memories to synthesize one that has more rows. As before let us assume that we are given chips of 2K rows with 4 bits/row. Now we want to build a device that has 4K rows with 4 bits/row. So:
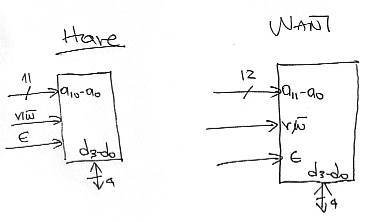
Again, looking at capacity alone we can see that we need at least two of the devices. The idea here is to map half of the addresses of the larger device to one of the smaller ones and the other half to the other smaller device. For example, in the diagram that follows we have mapped addresses of the form 0X...X onto the first device (top) and addresses of the form 1X...X to the second device (bottom). The way we achieve this mapping is by selectively activating one of the two using a 1-to-2 decoder and two AND gates. The AND gates drive the E signals. The top device will see an activated E only if the external E is 1 and A11 is 0. This is the case when an address of the form 0X...X is being accessed. Similarly, the lower device will see an active E signal only if the external E is 1 and A11 is 1 (hence when an address of the form 1X...X is accessed):
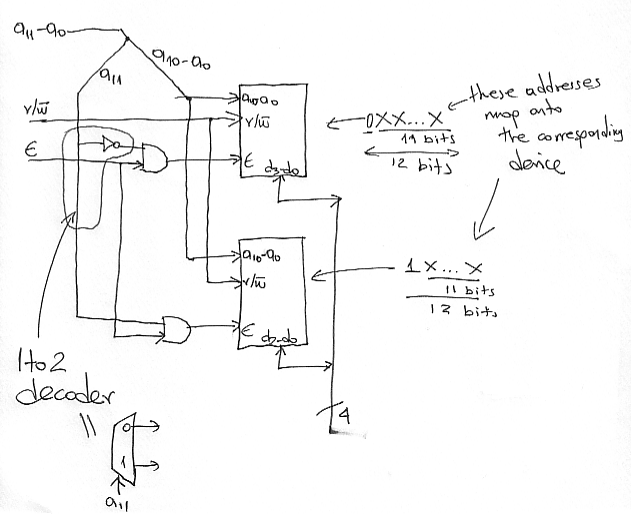
The corresponding data lines are tied together. At any given point of time only one of the devices reads these lines or drives them (on a memory write or read respectively).
Putting it all
together: Building a Wider and Taller Memory
As the last example letís see how we can build a device that has more rows and columns. Assume that we are given devices that are 16k rows x 4 bits (8Kbytes capacity) and we want to synthesize a device that has 64K rows with 16 bits per row. Capacity-wise we can calculate that we need eight of the smaller devices. They will be organized in a tiled fashion as follows:
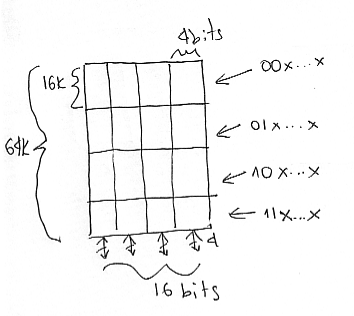
To decode the external addresses and map them to the row device rows we will need a 2-to-4 decoder. We will use address bits a15 and a14 for selecting one of the four rows. Hereís the complete diagram:
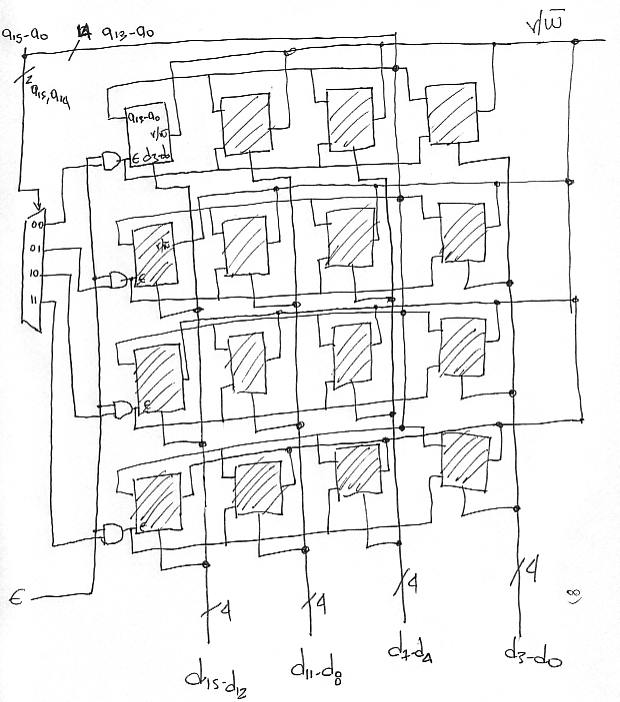
Which address bits
to use for address decoding? Necessity of Choice?
In the previous examples, we have used the most significant bit(s) of the incoming address to select a row of devices. In the previous example, 1/4 of the addresses were mapped to the top four devices, the next 1/4 to the next four devices and so on. This was by choice. We could have picked any pair of address bits to do the mapping. For example, we could have used the lower two address bits a0 and a1. In this case bits a15 through a13 (external) would have to be connected to the a13-a0 bits of the smaller devices and bits a0 and a1 (external) would drive the 2-to-4 decoder.
Interleaving:
The mapping of external addresses to internal devices is called interleaving. In the second scheme we described, addresses that are divisible by four map to the top devices, addresses that produce a remainder of 1 when divided by four would map to the second four devices and so on. This form of interleaving is often used in high-performance memory systems. There are two issues that must be explained to understand why this choice is made:
1) Memory devices are characterized by latency and cycle times. Latency is the amount of time it takes for memory to respond to a request. Cycle time is the total time necessary before another request can be made. Because reads are destructive operations the memory needs to rewrite the value read internally and that takes time (there are other considerations such as precharging the bitlines that contribute to cycle time). Think of this as asking someone to go fetch something. The time it takes for them to come back with what you asked is the latency. However, assuming that they were really nice and wanted to please you they ran, so now they are tired and need to catch a breath before being ready to serve another of your requests. This is the cycle time.
2) Often programs access memory addresses sequentially. That is if they access address 1, then the next access would probably be at address 2 and so on (think of sequential sequencing for instructions and of arrays for data).
With the interleaved mapping we just described, an access to address 0 will be serviced by row 00. After responding to the request, the row 00 devices will have to spent additional time (as explained for cycle time). If the next request is at address 1, then it would map to row 01 devices and hence the access can start immediately. With the first mapping (that used the upper bits for decoding) addresses 0 and 1 would map both onto row 00 hence the second access would need to observe the full cycle time of memory.
This is an example of a class of performance enhancing techniques. The principle here is the following: Study programs and determine a behavior that appears to be common (e.g., often accessing addresses sequentially). Build/organize devices that exploit this behavior to improve performance (e.g., interleave). These techniques are probabilistic in nature in that they *may* improve performance. They success lies in the assumption of a specific behavior. If the application that runs on the computer exhibits this behavior, then the technique is useful otherwise it may not be. Caches are another example of such a technique. They will be the topic of a set of upcoming lectures.