Andreas Moshovos

Fall 2007, Updated Fall 2008

Introduction to the NIOS II programming model

As noted in the previous lecture we will be talking about how NIOS II is supposed to behave. This is the programming model, or in other words the information provided here is a set of rules that should be used to interpret the machine’s behavior. A correctly implemented NIOS II must abide by all these rules. That is, a programmer can view this model as a contract between them and the designer. If the programmer follows these rules then their program must behave as expected on any implementation of NIOS II. From the designer’s point of view this is the minimum set of guarantees that they should provide. They are free to deviate on anything else but an implementation that breaks the programming model is not a correct implementation and should not be called NIOS II. This model is also typically called the Instruction Set Architecture. We will return to this term later on.

General Notes about Computer Structure and Operation:

As we discussed earlier, a simplified computer in general comprises three major parts:

1. The central processing unit or CPU or processor

2. Memory

3. Set of I/O devices

We have presented the memory behavior model in the previous lecture. We will discuss I/O devices later on. In this section of the lectures we will be concentrating on the CPU.

The CPU comprises two parts:

1. The datapath

2. The control

For the time being suffices to say that datapath is where data is stored and manipulated whereas the control is what orchestrates the datapath to perform all necessary actions. This information is provided just for reference for the time being, we will return to this issue when we discuss how to design a CPU that works.

What a CPU does:

In general terms a CPU goes through a series of steps repeatedly. These steps are:

1. Get next instruction

2. Decode (i.e., interpret its meaning) the instruction

3. Read Source Operands

4. Perform Operation (e.g., add two numbers)

5. Write Result

6. Determine which is the next instruction

All aforementioned steps together are called instruction execution. Depending on the instruction some steps may be optional (i.e., writing a result). We will see examples as we move along.

What is an instruction?

In the previous discussion we have used the term instruction. An instruction defines an operation that the CPU knows how to perform. For example, an instruction can be something like “add two numbers”. Each processor has a predefined set of instructions that it understands. The set of these instructions is part of the programming model so it is part of the instruction set architecture.

In addition to the instructions the programming model includes additional information such as where the operands of an instruction can be, what is the address space of memory, what datatypes are supported, etc.

There is no clear rule on what should be part of the programming model. A good design principle, however, is to include the minimum possible set of rules that allows a programmer to reason about the machine. Note that anything you put into the programming model becomes part of a contract and has to be supported in all implementations.

The NIOS II Programming Model

So, now we are ready to talk specifics and introduce the NIOS II programming model. We are not going to be able to exhaust this topic in a single or even in two lectures since the instructions are part of the model and there quite a few of them. We will gradually introduce additional instructions over a set of lectures. Much of the information we will be discussing is also described in the “NIOS II Processor Reference Handbook” which is available on the course website. The relevant chapter is “Chapter 3: Programming Model”.

Let’s first describe the memory model NIOS II assumes. It comprises 2^32=4G addresses where each address is capable of holding a single byte. Each byte is addressable, i.e., it can be accessed separately.

Memory supports three data types:

1. A Byte = 8 bits.

2. A Half Word = 2 bytes = 16 bits.

3. A Word = 32-bits.

All half-word and word accesses must be aligned, i.e., their starting address is divisible by two and four respectively. NIOS II will signal an error on unaligned accesses (will discuss what happens then later on).

Besides memory NIOS II and pretty much all modern processors have another set of storage locations that hold binary information. These are called registers. They are much fewer registers (e.g., less than 64 are typical) than memory locations and for this they are much faster to access. In semiconductors, the larger a memory structure, the slower it becomes. At the time of this writing common memory devices have a latency of 50ns whereas a high-end register file with 32 registers has a latency of 300-500ps – of course, the implementation of NIOS II we are using is slower. Registers use different names than memory locations. In NIOS II there is no such thing as the “address of a register”. There is only the “name of a register”. NIOS II has the following registers:

1. 32 general purpose registers. Each holds 32 bits. These are used for data manipulation.

2. Six control registers. Each holds 32 bits. These are used to control how NIOS II reacts to exceptions and external requests for service (e.g., a button is pressed on the board). We will be explaining these issues in detail when we talk about interrupt handling.

3. A Program Counter register. It holds the address, or “points to”, of the instruction under execution.

For the time being suffices to say that:

1. The PC is used for instruction sequencing. That it is used to identify the location of the instruction being execute and to perform step 6 of the CPU loop (determine next instruction).

3. The control registers control I/O device interactions. We will explain this later on.

The names of the general purpose registers are r0 through r31. Register r0 is special in that is always holds the value 0. You can use it as source and as a destination. If used as a destination it will silently ignore any attempt to change its value from 0. There are two reasons why r0 is set to zero. First, it turns out from experience that often enough many operations are done with zero being one of the operands. Second, having zero as an operand allow us to synthesize operations using others. For example, A = B can be implemented as A = B + 0. This way we do not need two operations one for simple assignment (often called a MOVE) and one for addition. Just addition is good enough.

By convention some registers have pre-specified uses. This means that while anyone is free to use them any way they like (there are no restrictions imposed by the hardware), if you want your software to inter-operate with software written by others it is important to abide by these conventions.

The following table lists these uses (you are not expected to understand every description at this point – most will be understood later on when we talk about how function calls are implemented):

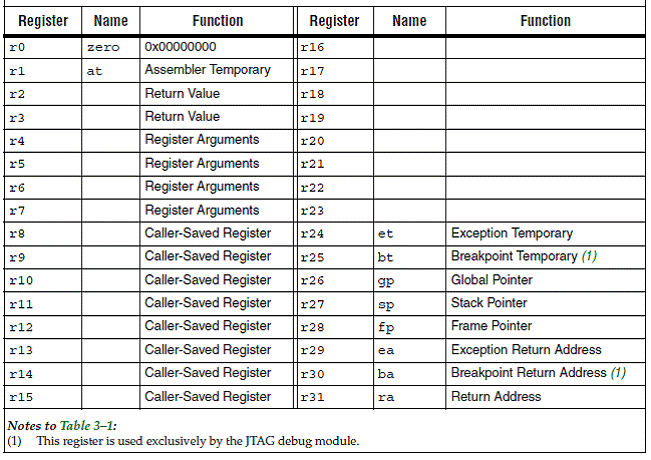
For your assembly programs it is safe to use registers r8 through r23. As shown on the table some register have aliases. For example, register “r0” and register “zero” refer to the same register. For the time being avoid using, all but registers r8 through r23.

Note that there is nothing inside the registers that signifies what the binary quantify they are holding is used for. That is, for example, are the contents of register r9 a number used for addition or an address used to access memory? It is us that decide what these quantities mean. To the computer they are just binary quantities that can be manipulated in specific ways using instructions. And again, there is nothing that differentiates the contents of register as an address. Only if those contents are sent to memory for reading or writing then they are *used* as an address.

There is no such thing as a register address. Registers have names. They are represented as digital numbers internally, but there is not way to take the result of an instruction and use that as the name of a register. This is in contrast to memory where, as we will see shortly, we can take the result of an addition or any other instruction and use that as an address to access memory.

We will be describing how NIOS II encodes instructions later on. For the time being, suffices to say that a NIOS II instruction is represented as a word value in memory. That is, all NIOS II instructions are encoded using 32-bit values.

Our first NIOS II program

As we saw before, the CPU loop amounts to executing instructions continuously. Before explaining how this is done let’s look at a simple program. For the time being we will not be concerned with how the program gets represented inside the machine or how it is executed. We will write a set of instructions and explain what the expected outcome should be. Once this is understood we will then explain where these instructions are stored, how they are sequenced and finally how they are represented.

Our first program will be the equivalent of the following pseudo-C code:

unsigned int a = 0x00000000;

unsigned int b = 0x00000001;

unsigned int c = 0x00000002;

a = b + c;

This code adds two 32-bit variables (b and c) and places the result into a third variable a.

While in C there is no indication of where the values are stored (C does not care) in a real machine the variables will have to be stored either in memory or in registers (there is nowhere else to store them). The compiler makes the decision on where to allocate each variable (if you want to force the compiler to allocate the variables in memory you can use the keyword “volatile” before each declaration).

Register Only Version

Let’s first see how we can implement our simple program assuming that the variables are in registers: a is in r9, b in r10 and c in r20.

If we want to add the contents of r10 and r11 and place the result into r9 we can use the following instruction:

add r9, r10, r11

Note that this does not affect the contents of r10 or r11. It reads the contents of r10 and r11, adds these up and then stores the result in r9.

In general, most NIOS II instructions take the following symbolic form:

operation destination, source1, source2

They instruct nios to perform:

destination = source1 operation source2

To complete our program we must first initialize b and c to 0x1 and 0x2 respectively. Here’s the complete code to do that:

addi r9, r0, 0x1

addi r10, r0, 0x2

add r8, r9, r10

“addi” stands for “add immediate”. It’s the same as “add” with the only difference that the second operand is a number.

Here’s what this sequence of instructions does:

The first instruction adds r0 and the value 0x1 and places the result (which is 0x1) in r9.

The second adds r0 and the value 0x2 and places the result in r10.

The third instruction adds r9 and r10 and places the result (0x3) into r8.

For the time being it is convenient to think that the instructions perform the following actions (semantically this is what they do, an implementation may choose to use a different, yet equivalent set of actions):

addi r9, r0, 0x1

1. Read r0

2. Add the value read in step 1 with 0x1

3. Write the value produced in step 2 in r9

4. Increment the PC to the next instruction

5.

addi r10, r0, 0x2

1. Read r0

2. Add the value read in step 1 with 0x2

3. Write the value produced in step 2 in r10

4. Increment the PC to the next instruction

add r8, r9, r10

1. Read r8

2. Read r9

3. Add the values read in steps 1 and 2

4. Write the value produced in step 3 in r8

5. Increment the PC to the next instruction

32-bit Constants?

What if we wanted to implement the following addition:

unsigned int a = 0x00000000;

unsigned int b = 0x11223344;

unsigned int c = 0x55667788;

a = b + c;

Unfortunately, the number operand in “addi” can only be 16-bits. NIOS-II first sign-extends this number to 32-bits and then performs the addition. So, “addi r8, r9, 0x8000” is equivalent to “r8 = r9 + 0xFFFF8000”, whereas addi r8, r9, 0x7000 is equivalent to “r8 = r9 + 0x00007000”. The encoding of addi in memory is as follows:

Where A and B are the two register operands; B is the destination register and A is the source. Imm16 holds the 16-bit immediate field. The last 6 bits are 0x04 which tells NIOS II that this is an addi instruction.

So, how do we go about implementing the addition in this case? We’ll need two instructions to construct the 32-bit numbers.

Here’s how we write 0x11223344 into r9:

movhi r9, 0x1122

ori r9, r9, 0x3344

“movhi r9, 0x1122” does r9 = 0x11220000. In general “movhi r9, 0xYYYY” does r9 = 0xYYYY0000, where YYYY can be any 16-bit number expressed in hexadecimal. In more words, movhi sets the lower 16-bits of the destination to zero and the upper 16-bits to the 16-bit source operand.

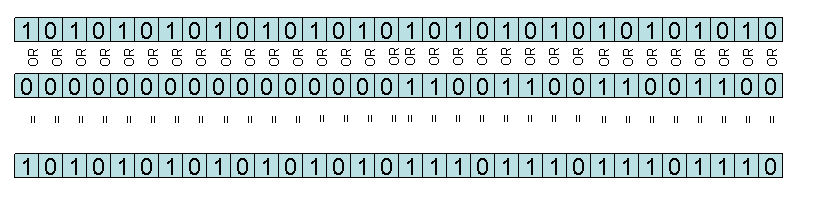
“ori r9, r9, 0x3344” does r9 = r9 bitwise-OR 0x00003344. Bitwise OR works at the bit level by ORing (in the Boolean sense) the corresponding bits of r9 and of the immediate in pairs. So bit 0 of r9 will be ORed (in the Boolean algebra sense) with bit 0 of the immediate and the result will be written to bit 0 of the output. This is done for bits 0 through bit 15 since the immediate is 16 bits. The upper 16 bits (bits 16 through 31) are copied as-is from r9 to the output.

Here’s the calculation that takes place when we execute ori r9, r9, 0xcccc when initially r9 holds the value 0xaaaaaaaaaa. Note that 0xcccc = 1100 1100 1100 1100 in binary and 0xa..a = 1010 ... 1010 in binary.

Here’s the complete code:

movhi r9, 0x1122

ori r9, r9, 0x3344

movhi r10, 0x5566

ori r10, 0x7788

add r8, r9, r10

“movhi rX, Imm16” is an pseudo-instruction. It gets translated into “orhi rX, r0, Imm16”. “Orhi rX, rY, Imm16” bitwise ORs the 16 bit immediate with the upper 16 bits of rY and stores the result in rX. By using rY=r0 we effectively store the Imm16 in the upper 16 bits of rX while zeroing out the lower 16 bits of rX.

Instead of using the orhi and ori sequence to create a 32-bit constant we can instead use the movia pseudo-instruction. So, “movia r9, Imm32” stores the 32-bit immediate Imm32 in register r9. The sequence of instructions movia translates to is slightly different than what we described here. It uses an addition instead of an or as the second step. At some point we will explain it.

NIOS II assembly includes several pseudo-instructions for creating numbers:

1. movi rX, Imm16 --> rx = sign-extended(Imm16) where Imm16 is a 16-bit immediate

2. movui rX, Imm17 --> rx = zero-extended(Imm16)

3. movia rX, Imm32 --> rx = Imm32

Memory Version

What if we wanted the variables a, b, and c to be stored in memory?

NIOS II is a load/store architecture. That is, all data manipulation happens in registers. To add b to c we must first read the values into registers, do the addition in registers and then write the result back to memory.

Let’s assume that we allocated a through c in consecutive memory locations starting from address 0x00200000 (this address is valid on the DE-2).

So the relevant part of memory will look as follows:

Address	+0	+1	+2	+3
0x00200000	0x00	0x00	0x00	0x00
0x00200004	0x44	0x33	0x22	0x11
0x00200008	0x88	0x77	0x66	0x55

“a” is in memory locations 0x00200000 through 0x00200000, “b” is in 0x00200004 through 0x0020007, and “c” is in 0x00200008 through 0x0020000c.

Here’s the full program. This is not the shortest possible program. We will soon see how we can eliminate some of the instructions.

movhi r11, 0x0020

ori r11, r11, 0x0004

ldw r9, 0x0(r11)

movhi r11, 0x0020

ori r11, 0x0008

ldw r10, 0x0(r11)

add r8, r9, r10

movhi r11, 0x0020

ori r11, r11, 0x0000

stw r8, 0x0(r11)

The first three instructions read b from memory into r9, the next three read c from memory into r10, the next instruction adds r9 and r10 into r8, and the last three instructions write r8 to memory. The new instructions here are ldw and stw. They take the following form:

ldw rX, Imm16(rY)

stw rX, Imm16(rY)

Where rX and rY are registers and Imm16 is a 16-bit constant. Let’s look at the ldw. It does the following

1. Read rY

2. Sign-extend Imm16 to 32 bits

3. Add the values of step 1 and 2

4. Read from memory a word (32 bits) using the value produced in step 3 as the address

5. Write the value read in step 4 into register rY

So, the first three instructions read from memory location 0x002000004 a word into register r9. The first two form the value 0x00200000 into r9 and the ldwio uses r9 to read from memory.

In short hand notation “ldw rX, Imm16(rY)” does:

Rx = mem[rY + sign-extended(Imm16)]

“Stwio” is similar to “ldw” and differs only in that it performs a memory write. “stw rX, Imm16(rY)” does the following:

1. Read rY

2. Sign-extend Imm16 to 32 bits

3. Add the values of step 1 and 2

4. Write from memory the value of register rX using the value produced in step 3 as the address

In short hand notation “ldw rX, Imm16(rY)” does:

mem[rY + sign-extended(Imm16)] = Rx

Let’s now look at our program and understand what each instruction does:

movhi r11, 0x0020 à r11 = 0x00200000

ori r11, r11, 0x0004 à r11 = 0x00200000 OR 0x0000004 = 0x00200004

ldw r9, 0x0(r11) à r9 = mem[r11 + sign-extend(0x0)] = mem[0x00200004] = 0x11223344

movhi r11, 0x0020 à r11 = 0x00200000

ori r11, 0x0008 à r11 = 0x00200000 OR 0x00000008 = 0x00200008

ldw r10, 0x0(r11) à r10 = mem[r11 + sign-extend(0x0)] = mem[0x00200008] = 0x55667788

add r8, r9, r10 à r8 = r9 + r10 = 0x11223344 + 0x55667788 = 0x6688aacc

movhi r11, 0x0020 à r11 = 0x00200000

ori r11, r11, 0x0000 à r11 = r11 OR 0x00000000 = 0x00200000

stw r8, 0x0(r11) à mem[r11 + sign-extend(0) = r8, that is mem[0x00200000] = 0x00200000

Addressing Modes

On a final note, the term addressing mode describes a way of specifying an input or output operand for instructions. In this lecture we have seen three addressing modes.

1. “Register”, as in add r10, r9, r2. All three operands are registers.

2. “Immediate”, as in the last operand of addi r8, r9, 10.

3. “Register Indirect with Displacement” as in the second operand of ldw r10, 0x4(r9). The name is a bit unfortunate as it fails to explicitly state that we are referring to memory. The name describes how we calculate the memory address referenced. It’s “register indirect” because we are using a register’s value to refer to memory. This is akin to a pointer in C. The “displacement” implies that we add a displacement, i.e., a constant to the register value prior to using it to access memory.

Another addressing mode is “register indirect” which in NIOS II is simply “register indirect with displacement” where we use a displacement of zero. In other architectures there are other addressing modes. We will talk about some of these much later.

Memory Version – Take 2

We will cover this later on in the course:

We can replace the first three instructions:

movhi r11, 0x0020

ori r11, r11, 0x0004

ldw r9, 0x0(r11)

with:

movhi r11, 0x0020 à r11 = 0x00200000

ldw r9, 0x4(r11) à r9 = mem[r11 + sign-extend(0x4)] = mem[0x00200000 + 0x00000004] = mem[0x00200004] = 0x11223344

Here’s a new shorter version:

movhi r11, 0x0020

ldw r9, 0x4(r11)

ldw r10, 0x8(r11)

add r8, r9, r10

stw r8, 0x0(r11)

Note that the value of r11 remains constant as 0x00200000 after the first instruction and subsequent loads uses their immediate operand as an offset from that value.

Note that in the previous example we exploited the addition that ldw and stw perform as part of their address calculation. In general, when we want to access from memory location A we can use the following sequence:

movhi r11, Upper 16 bits of A

ldw r9, Lower 16 bits of A(r11)

Care must be taken when bit 15 (the 16 bit of A) is 1. This is for example the case with A=0x208000. The following sequence does not access address 0x208000:

movhi r11, 0x0020

ldw r9, 0x8000(r11)

The problem is that in this case, the lower 16 bits of A are 0x8000. The addition which ldw performs as part of the address calculation will sign extend this to 0xFFFF8000. Adding that to 0x00200000 (the result of movhi) produces 0x001F8000. In this case, the constant used by movhi must be adjusted by adding 1 to it. So the correct sequence is:

movhi r11, 0x0021

ldw r9, 0x8000(r11)

Fortunately, you do not have to do these conversions by hand. You can instead use the macros %hiadj(Imm32) and %lo(Imm32) where Imm32 is a 32-bit immediate. %lo(Imm32) returns the lower 16 bits of Imm32. %hiadj(Imm32) returns the upper 32 bits of Imm32. It adds 1 to those if bit 15 of Imm32 is 1.