Computer Organization
Using Bits to Represent
Things
Andreas Moshovos
Spring 2004, Revised: Spring 2006, Spring 2008, Spring 2010, Fall 2022
In this section we will be *reviewing* ways in which different things can be represented in a computer.
As we discussed, in a computer everything is interpreted as 0 or 1. In real life we have to manipulate a lot more than just two things. For example, the English alphabet has more than just two characters. Accordingly, it would be nice to be able to manipulate numbers other than just 0 and 1.
The key mechanism via which a computer can manipulate larger quantities is by using a collection of multiple bits. A bit is a single binary digit and can take the values 0 and 1. Using multiple bits we can represent one of many possible things. For example, say I want to be able to represent the letters A, B, C and D. I can design my computer and my programs such that A is mapped onto 00, B onto 01 and so on. Using two bits collectively I’m able to represent four different things. It is important to clarify that internally the computer really knows about 00, 01, 10 and 11. It does not understand A, B, C, or D. We, as humans, are able to do the mapping and understand that whenever 00 appears this really means A. Some of the operations that the computer can perform are designed assuming a specific meaning for the data they manipulate. For example, a computer can do addition. In this case, the operation interprets the two input binary quantities as numbers and manipulates them as if they were numbers. These data types that are supported by the computer’s operations can be called intrinsic datatypes. A typical processor will support operations on integer numbers of different lengths (more on this next). Other data types may or may not be supported directly by the hardware. Most computers today support operations on integers and on approximations of real numbers called “floating-point” numbers (more on this later).
By using N bits we can represent up to 2^N different things. So, with two bits we can represent four things. With eight bits we can represent 256 things.
Review of K/M/G/T: Often in binary systems we talk about 1K, 1M, 1G or now days about 1T. These multiplication factors are very handy. Turns out that it is fairly straightforward to remember what they mean:
1K = 2^10, 1M = 2^20, 1G = 2^30, 1T = 2^40, 1P = 2^50, where K = kilo, M = mega, G = giga, T = tera, P = peta. So K is the number of things you can represent with 10 bits, M the number of things you can represent with 20 bits and so on.
Given a collection of N bits, we typically write the bits from left to right, e.g., 10101010. The leftmost bit is called the Most Significant Bit (MSB), while the rightmost bit is called the Least Significant Bit (LSB). This naming makes sense if one considers how numbers are typically represented in computers which is the next topic that we will discuss.
Representing Physical Numbers: A quantity that computers usually manipulate is a number. This requires a way of representing numbers inside a computer and to be able to perform arithmetic operations on them.
We could use *any* mapping of binary quantities to numbers. Say, for example, I was given two bits. I could, if I wanted to, define the following mapping:
00 is 3
01 is 2
10 is 1
11 is 0
The important point here is that the meaning we give to binary numbers or numbers is a choice that we, or others, have made. Any mapping *is* correct and will work just fine so long as we interpret it correctly. Some representations are easier for people to learn and use, others may be easier to design circuits for. These factors are best taken into account before we decide which representation "we feel like" using.
Now forget about the aforementioned mapping and let’s talk about what is used in practice today. Again, it is important to understand that our discussion centers on the *convention* that everyone has agreed upon using to represent numbers by using binary quantities.
A convenient way of representing numbers is the one we are all accustomed to from the decimal system. Please recall that for most of us it took a while to learn what decimal numbers mean and how to do simple math operations with them. Let’s take a look at the decimal system. Say we have the number 956. What does it mean? We were all trained to interpret this as 9x100+5x10+6x1. Written differently this is 9x10^2+5x10^1+6x10^0. In other words, every digit is multiplied by the base (10 in this case) raised in the power of the digit’s position. This is why this number representation is a positional representation. The rightmost digit is at position 0, the one on its right is at position 1, and so on. The very same method is used for binary numbers and is the common method of representing numbers in digital systems. So, if I’m given the binary number 1010 how do I interpret it? It’s 1x2^3+0x2^2+1^2^1+0x2^0 or 8+2 = 10 in decimal.
In general, if I have an n-bit number with digits B(n-1)B(n-2)...B(0) the number is B(n-1)x2^(n-1)+...+B(0)x2^0 in decimal.
This representation is sufficient for representing physical numbers. That is positive integer numbers and zero. Addition is identical (in its process) to addition with decimal numbers. So:
0100
+0110
-----
1010
We start from right. We add the two digits of the current column. There are two outcomes: (1) The sum digit which we write underneath, and (2) the carry which we use when we add the bits of the next column. The sum and the carry can only take the values 0 or 1.
As a sidenote, if you have time at some point (not directly related to the course), it would be interesting to try to read about the history of counting or numbering systems. Things that we take for granted such as the positional representation, the use of the base 10 system, and the existence of zero, took a while to develop.
Fixed
Length Representation and its implications
Let’s deviate a bit a talk about number length/precision. When we manipulate numbers on a piece of paper it is straightforward to write a number as large as we like. For example, adding 999 and 111 gives a number with four decimal digits (1110). We can just use the extra space on our paper, or get a longer paper, to write that extra 1. Inside a computer, however, every bit is represented using storage elements and communicated through wires. At design time, a decision is made on what is the *maximum* number that can be stored inside a particular storage element and that can be manipulated by the various functional units (e.g., the unit that does addition). The largest data type that a computer can manipulate is often used to characterize the whole computer system. So, for example, early microprocessors/personal computers were 8-bit because the maximum quantity they could manipulate in a single operation was just 8 bits. If one wanted to manipulate wider quantities they had to write an algorithm/program to do so, or in other words, they had to synthesize operations for quantities larger than 8 bits. More recent microprocessors were capable of operating on 16-bit quantities. Today most microprocessors are 64-bit. Please note that we are talking about physical numbers for the time being. Also note that 2^64 is a very large number (once I was told that there are not that many molecules in the universe but I’m still counting).
For most of this course we will not be using 64-bit quantities. But the concepts apply to all processors. We will be focusing mostly on 32-bit numbers or shorter.
It is important to remember that only a fixed range of numbers can be represented directly in a, say, 32-bit quantity. So, as long as we are talking about physical numbers this range is 0...(2^32-1) (or 0 to 4G). It is possible when adding two numbers to get OVERFLOW. This happens when the result requires more digits for its representation that those that are available to us. In this case it is impossible to represent the number directly. Most computers will provide a mechanism for identifying such results and allow us to take special action if we so desire. Typical adders (circuits that do addition) turns out that they perform modulo addition. That is, they operate very much like the kilometer counters found in older cars. As soon as the result gets over “9999”, or, more appropriately 1111 for binary counting, they wrap-around to 0 and start over from there. So, a 32-bit adder does addition modulo 2^32, i.e., it really calculates (a+b)MOD 2^32 as opposed to a+b.
In C and C++ physical numbers can be declared as “unsigned int” or “unsigned short” or “unsigned long”. The exact length of the number you are getting depends on the system. On a P4/Core/Athlon PC, these correspond to 32, 16 and 32 bit respectively. There is also “unsigned long long” which typically corresponds to a 64-bit quantity.
A final implication of the fixed-length representation is that a number is always represented with the same number of bits no matter what, so there may be leading zeroes. For example, if the representation used is 8-bits wide, the number 32 is stored inside the computer as “0010 0001”. The first two leading 00 are also there (the space in between is for our reading convenience – it’s not there in the computer). This in contrast to the way we write numbers on a piece of paper. If your boss comes and says that your salary will become 099.25/hour as opposed to 99.25/hour you shouldn’t be making big plans with what to do with that extra 0 income.
Back on the issue of representation:
Negative/Integer
Numbers:
For practical reasons it is also nice to be able to represent negative numbers in a computer. When we write on a piece of paper this is fairly “easy”. Just put a minus in front of the number, spend one or two years in primary school to learn how to manipulate these numbers, and voilà, we are done. Unfortunately, this is not going to work for a computer. As we said, a computer only “knows” 0 and 1 nothing else. Hence, if we are to represent minus we have to use a binary quantity.
One easy to understand but practically very inconvenient way of representing numbers is the sign-magnitude representation. We only discuss because a variation of it is used for representing approximations of real numbers (more on this later). In the sign-magnitude representation the most significant bit is the sign and the rest is the weight of the number. Assuming, say a 5-bit signed number we have a representation of “S W3 W2 W1 W0” and the number is (-1)^S x W3x2^3+W2x2^2+W1x2+W0. Note that (-1)^0 = 1 and (-1)^1 = (-1). So, 10010 is -2 and 00010 is 2. While fairly straightforward for us humans, it turns out that the circuits required to do addition using this representation are quite complicated (we have to check the signs of the two numbers – if they are of the same sign, we can perform addition. Otherwise, we have to perform subtraction in which case, we have to worry about which number has the highest magnitude/absolute value. The circuits ends up implementing a if-then-else statement in hardware which is not very efficient nor fast. So, this representation is not commonly used in practice.
The representation that is used in practice is 2’s complement. The easiest way to understand 2’s complement is to start by taking for granted that a typical simple adder does modulo addition (something we mentioned before). So, say I have a 3 bit adder and I add 3 and 5. 3 in three bits is 011 and 5 is 101. The result is going to be 1000 but because there are only three bits in the adder outcome we are going to get just 000. So, as soon as we exceeded the maximum of 7, our adder wrapped to 0 and started from there. Similarly adding 3 and 6 produces 001. Take this for granted for the time being.
So, now that we know how our circuits work, let’s try to find a representation of negative numbers that would produce the expected outcome for signed numbers. Returning to fundamentals, recall that given a number A its negative –A is defined as a number such that A+(-A)=0 (told you, we will be using high-caliber math here). So, why not define –A to be that number that when added to A produces 0 in modulo addition? For this it’s convenient to draw a circle with the numbers on it (we’ll do this in class). Turns out that for 3-bit numbers we can define -1 to be what otherwise we would consider as 7 if it was a physical number. This is because 001+111 results in 000. Similarly, -2 is 110, -3 is 101. There are not enough digits to represent 4, but we are able to represent -4 using 100 (this is convenient as now all negative numbers have a most significant bit of 1 whereas all positive numbers have an MSB – Most Significant Bit - of 0). With 3 bits we are able to represent integers in the region of -4 through +3. In general with n bits we can represent numbers in the region of -2^(n-1) through +2^(n-1)-1. Notice that there is an asymmetry as we are able to represent 2^(n-1)-1 positive numbers and 2^(n-1) negative numbers. This is because one combination is used for zero.
The nice thing about 2’s complement numbers is that we can manipulate them directly using a regular adder.
Subtraction is now possible by first converting the second number into its negative and then adding, i.e., a-b = a + (-b).
Given a number, we cannot directly tell what it represents. To correctly interpret a number we first look at its MSB (leftmost bit). If it is 0 then this is positive number and the remaining bits provide its weight. So, 0010 is +2. If the MSB is 1 then this is a negative number and we have to take the 2’s complement to find its weight. So 1101 is a negative number because it is of the form 1XXX (X is usually used to represent the “any possible value”, sometimes it is also used to represent the “don’t care can take any value”). How do we find the 2’s complement of a number. There two ways:
Way #1. To find the 2’s complement of A, calculate NOT(A) and add 1 (NOT(A)+1). So, for 1101 we have NOT(1101) = 0010, add 1 to this and we get 0011. Thus, 1101 is really -3.
Way #2. This is really a shortcut way and is pretty handy and you do not have to do an addition. The rule is start from the right side of the number copying digits unit you hit the first non-zero digit. Copy the first non-zero digit and then reverse all remaining digits. So, in our example of 1101, we start from left and the first non-zero digit is the first 1, we copy that and then reverse the rest 110 becomes 001. At the end we get 001 (the reversed part) and the 1 (the copied part) or 0011. So, what number is 111010? 0001 (reversed) and 10 (copied) or – 000110 or -6.
2’s complement and over/underflow: As with physical numbers we can only represent a fixed range of signed integers. It is thus possible to get overflow (very large positive number) or underflow (very small negative number) when doing calculations with these numbers. How can we tell that this has happened? As a rule of thumb when we add two numbers that have different signs it is not possible to have over/underflow. Only when we add numbers of the same sign this may happen. You can detect this when the result has a different sign than that of the two numbers that are being added. Again, this is convenient from a human perspective. From a circuit perspective the following is much more convenient: if the carry into the last pair of digits is different than the outcome out of that pair then we have over/underflow. For this course we do not care to prove that this is correct.
In C/C++ 2’s complement numbers can be declared using “int”, “short” or “long” that is by dropping the “unsigned” part.
In summary, with an n-bit quantity we can represent the unsigned numbers 0 to 2^n-1 (2^n numbers in total), and the signed numbers -|2^(n-1)| through 2^(n-1)-1 (again 2^n numbers in total). For example, for n=8 we can represent the numbers 0 to 255 when the 8-bits are interpreted as an unsigned number. For a signed interpretation we can represent -128 to 127.
The following figure shows how signed and unsigned numbers are mapped using a number scale where on the leftmost end we have the number comprising all zeroes and on the rightmost end we have the number comprising all ones:
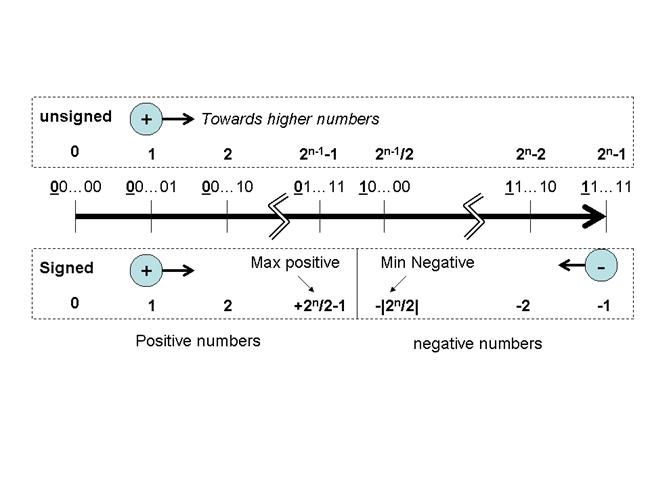
If you were to think of the
numbers being on a donut with 0…0 being at the 12 o’clock
position, then the following holds:
1. For unsigned numbers, as we move clockwise making steps one
value at a time, the magnitude increases. At six o’clock
we have 10…0, and just before wrapping around back to 0…0, we have 1…1, which
is the maximum possible number, 2^N-1 where N the number of bits used.
2. For signed numbers, all is the above, up to and including the
number before the 6 o’clock position, 01…1. In this case, 01…1 is the maximum
positive number 2^(N-1)-1. One more step, and we end
up again at 10…0. But now this the smallest possible negative number -2^(N-1). Or in other words, the
negative number with the largest magnitude. As we keep moving clockwise,
eventually we arrive just before 0…0 at 1…1 which is
-1. One more step, and we are back at 0…0.
Sign Extension
In C, C++, you can write this:
short i16 = 256;
char i8 = -1
i16 = i16 + i8;
Recall that typically a short will be a 16 bit quantity whereas a char will be a byte/8 bit quantity. One would expect that the addition would produce the result of 256+(-1) = 255. After all, why should we care whether we use 8 or 16 bits to represent an integer? The addition should work as expected.
However, additional care must be taken before operations between representations of different lengths can take place. Specifically, in this case the binary representations of the initial values are:
i16 = 0000 0001 0000 0000
i8 = 1111 1111
Let’s try to add them up. Notice the empty space in i8? There is nothing there. But then we try to add i8 to i16, what should we do? Should we just ignore the “missing” bits, fill them with zero, or do something else?
Let’s try the fill them with zero (ignoring, i.e., just copying the upper 8 bits of i16 produces the exact same result in this case):
i16 = 0000 0001 0000 0000
i8 = 1111 1111
---------------------------
+ = 0000 0001 1111 1111
What is the result? It is a positive number (since the MSB is 0) and its value, if you do the conversion to decimal, is 511. That’s not the 255 we expected.
For the addition to work, we have to convert the number with the shorter representation, to a representation that has the same length as the other number. In the case of signed numbers (integers) this is called sign extension. What do in sign extension is to copy the MSB bit to all the vacant positions. So, starting with i8 we take it’s MSB which is underlined here 1111 1111, and copy as many times as necessary to generate a 16 bit number: 1111 1111 1111 1111. If you interpret now this 16-bit quantity as an integer in 2’s complement you will see that it represents -1. Now do the addition and you will end up with:
1 0000 0000 1111 1111
^ this is a carry out and is discarded. So we are left with 0000 0000 1111 1111 which is 255.
If i8 was 0111 1111 (or 127) then sign extension to 32 bits would have produced 0000 0000 0111 1111, which is still 127 in 16 bits.
So, returning to our C statement, in reality what the computer does to perform the addition is the following
short temp;
temp = (sign-extend) i8; // this is pseudo-code, you can get the same effect by writing temp = (short) i8
I16 = i16 + temp;
Zero Extension
A similar issue to the one just describe applies to unsigned numbers. In this case, however, things are much simpler. Whenever we need to operate on two unsigned numbers of different lengths, we again convert the shorter number to the longer one, but in this case we can just fill in the vacant positions with 0. So, for example:
unsigned short i16 = 256;
unsigned char i8 = 10;
The binary representations are:
I16 = 0000 0001 0000 0000
I8 = 0000 1010
If we need to do i16 = i16 + i8, then we zero extend i8 (the zero extended digits are underlined) to 16 bits and do the addition:
I16 = 0000 0001 0000 1010
I8 = 0000 0000 0000 1010
-------------------------
+ 0000
0001 0000 1010
Which is 266.
Unfortunately,
there is no direct way of declaring binary numbers in C or C++. And this brings
us to the next topic:
Convenient
representations of binary numbers for humans, or, how to write long binary
numbers in a program:
When dealing with computers it is often necessary to declare/write binary constants. It is pretty inconvenient and error prone to write 32-bit binary numbers. For this reason, it is convenient to use the hexadecimal or the octal system. In the hexadecimal system each digit can take values from 0 up to 15. For practical reasons digits 10 through 15 are represented with A, B, C, D, E and F respectively.
The nice thing about the hexadecimal system is that because 16=2^4 each hexadecimal digit can be directly converted into a 4 bit number and vice versa. So, this way, writing down 32-bit constants results in a much more compact representation. In C we can specify hexadecimal constants using the 0x prefix.
So, 0xdeafbeef corresponds to the following 32-bit binary number
0000 111a 1010 1011 1011 1110 1110 1111
0 f a b b e e f
Of course, if the leading digits are zeroes we do not have to write them down. So 0x1 = 0x00000001. The 0x prefix is used to differentiate from decimal numbers as 109 is meaningful in both systems.
Things can get a bit ugly with the hexadecimal representation. Sometimes, it is not obvious how many digits are really there. For example, let’s say we have a 7-bit number which is 101 0001 in binary. You may see this been represented as 0x51 in hexadecimal. The leading 5 corresponds only to three bits in this case. How can you tell how many bits a hexadecimal number corresponds to? Someone has to specify that. It will often be clear from other information. All but the leftmost digit correspond to four bits. The leftmost digit can be representing anywhere from 1 to up to 4 bits.
Similarly to the hexadecimal system, the octal system where digits take the values 0 through 7 can also be used for compactly representing binary numbers. A single octal digit corresponds to a 3 bit number. In C octal constants are prefixed with 0. So, if you write 041 you are getting 4x8+1 = 33 and not 41.
How can a computer understand that a constant is in hexadecimal (hex for short) or in octal?
Well, it can’t because what we are talking about are representations that we humans can use to make our life easier. The compiler translates these representations into their corresponding binary form when these are eventually stored into the computer. So, it is important to clarify and understand that nowhere in the machine there will be a thing such as a hexadecimal or an octal number. There are going to be binary numbers whose values for convenience we can write or display in hex or octal form (a program will be required to do so). We could however store a string representation in ASCII of a hexadecimal/octal number. But that’s not a number it’s a sequence of characters that when you look at them *you* understand that it can be interpreted as a number. To the computer is exactly just a sequence of bytes.
Things
other than integers?
Besides numbers often times it is necessary to represent other quantities. A commonly set of things that we have to represent consists of the symbols we use for writing (AKA letters, number digits, punctuation symbols, etc.). This is so common that a representation has been standardized. This is the ASCII. ASCII uses 7 bits (or an 8-bit number whose upper bit is 0) to represent characters, digits and other punctuation marks such at the dot the comma, etc. Space is number 32, the digit 0 is the number 48, digit 1 is 49 and so on. The letter a is number 65 while b is 66. Numbers lower than 32 are reserved for non-printable symbols. In a typical system control characters map to these numbers. For example control-A is number 1. Depending on the device used to display the characters/symbols these control characters may correspond to actions such as moving down a line (10 or 11 I think) or going back a character (backspace or 8).
Strings:
Words can be represented a sequence of characters. These are called strings. There are two common representations of strings:
1. Zero terminated: The characters appear one after the other and the last character is always a 0. This is the default implementation of strings in C.
2. Length+characters. The first byte is a number indicating the length of the string (i.e., how many characters it has). The characters follow. This is default implementation in a language called Pascal that was used in the “old” days. In Java you could opt for this and depending on the library you may be able to get this in C++.
Note that for the time being we are not talking about where these things are stored. We will do this in the next lecture when we talk about memory.
FYI there are now extended representations of characters called UTF-X (where X a number) that can be used to represent symbols out of several different languages. The exact form of these representations is beyond the scope of this course. In the simplest representation a 16-bit quantity is used per symbol. In more compact representations, an escape character (a byte say that has the value all ones) is used as prefix to refer to extended characters.
In C you can declare a character by using the “char” or “unsigned char” keywords. I’m not aware of any standard way of declaring UTF characters. You have to synthesize the behavior using standard characters.
Fixed
vs. Variable Length Representations
And strings lead us to a parenthetic note about fixed vs. variable length representations. In all representations we talked about thus far, the actual number of bits used per character/number was fixed at design time and was implied. We know when we add two “unsigned int” numbers we are manipulating two quantities that are of 32-bits. The computer will know that too as we will explain how things like “do addition” are encoded inside a computer. This information is implied and embedded into the hardware design of the components involved (if we implement this say in a processor). Typical computer systems support a few, fixed length datatypes, such as 8-bit and 32-bit integers. This again is an engineering trade-off. The people that built the machines decided that it was better to use a few fixed data types and build circuits to manipulate those.
Alternatively, we could opt for variable length representations. Strings provided two examples of such representations. The zero terminated representation uses a “special” “end-of-item” marker (the zero byte) and the length+characters representation encodes the actual length inside the item itself. While in strings we use bytes as our minimum data quantity, in principle we could think of variable length representations that go down to the bit level. In fact, most compression and encoding methods do treat information as a bit stream and use variable length representations to maximize the amount of information that can be represented with a given number of bits.
Another example of variable length encoding we will see when we talk about how some processors encode instructions (i.e., the types of actions they can take).
Real Numbers: How can we represent things such as 1.3 into a computer?
One possibility is using a “fixed-point” representation. This is commonly used in embedded systems and there isn’t really a clear standard on the format of these numbers. A possible format is the following: Assume for clarity a 4 bit representation and let’s take for example the number 1100. In a fixed point representation the fixed refers to the fact that the “.” (the point) of the real number is at a fixed position with respect to the four digits. So the number is really 0.1100. Notice that the dot is placed immediately on the left of the four digits. So, the number is 1x2^-1+1^2-2+0x2^-3+0x2^-4 or 0.5 + 0.25 = 0.75. The smallest number we can represent is 2^(-4) (using 0001) and the maximum is 0 (using 0000).
Another possibility is using a “floating-point” representation. Fortunately, for this representation there are standards that are widely used. This is the IEEE 754 standard.
There are two representations with different precision. Let’s see the one that uses 32-bits.
Bit: 31 30 23 22 0
The most significant bit is the sign bit (S) above.
Bits 30 through 23 form the exponent which is unsigned integer.
Bits 22 through 0 form the mantissa which is also a number whose meaning will be explained next.
Modulo special cases (we will refer to them in a moment) the number being represented is:
(-1)^S x 2^(E-127) x 1.Mantissa
Notice that the 1. that appears in front of the mantissa is implied and is assumed to always be there. That “1.” does not appear in the binary representation.
This is best understood by an example:
1 10000001 10000000000000000000000
So S = 1, E = 10000001 = 129 and Mantissa = 10000000000000000000000
The number is then
(-1)^1 x 2^(129-127) x 1.10000000000000000000000 = -2^2 x binary(1.1) =-4 x 1.5 = -6.0
another example:
0 01111110 11000000000000000000000
is:
(-1)^0 x 2^(126-127) x 1.11 = 2^(-1) x 1.75 = 1.75/2 = 0.875
The IEEE Standard has a few special cases which are beyond the scope of this course:
If E=0,
M non-zero, value=(-1)^S x 2^(-126) x 0.M (denormals)
If E=0, M zero and S=1, value=-0
If E=0, M zero and S=0, value=0
If E=1...1, M non-zero, value=
If E=1...1, M zero and S=1, value=-infinity
If E=1...1, M zero and S=0, value=infinity
IEEE 754 defines also 64-bit floating-point numbers. There S is still a single bit, the exponent is 11 bits and the bias is not 126 but 2047, and the mantissa is 52 bits.
More recently, and partly because machine learning has become so prevalent, a half-precision floating-point format has emerged. It has a 5b exponent biased by 15, and 10b of mantissa. The double-, single-, and half-precision formats are also often referred to as FP64, FP32, and FP16. More recently (Fall 2022), FP8 formats have been proposed (see https://arxiv.org/abs/2209.05433). Bfloat16 is another 16b format that is in used in the tensor processing unit series by Google. It has an 8b exponent and 7b of mantissa.
In C/C++ you can get the 32-bit precision (single precision) using “float” and the 64-bit precision or double precision using “double”.
Use the following C program to see how different floating point numbers of single precision are represented on an x86 machine (change the value for f):
float f = 8.25;
unsigned int *c;
main ()
{
c = (unsigned int
*) & f; // this will allow us to use f as if it was an unsigned integer and
without any numerical conversion
printf ("%f is
represented as 0x%08x\n", f, *c);
printf ("The S
bit is %d\n", (*c) >> 31); // just keep the MSB
printf ("The
exponent is %d\n", ((*c) >> 22) & 0xff); // keep bits 31-23
printf ("The
mantissa is 0x%x\n", (*c) & 0x3fffff); // keep the lower 23 bits
}
Use this program for practice. Look at the binary representation and try to convert it back to decimal and see if your calculations match the program’s output.
Also, after reading the conversion section that follows, convert a couple of real numbers to floating point and use the program to check whether you got it right.
Finally, if you have lots of time in your hands see if you can follow the logic of the program and then try to convert this to work with double precision numbers. You may need to know that 64-bit constants can be declared using the ULL suffix (for unsigned long long). That is to get the number 123 but in 64 bits you need to write 123ULL, to get 0x1234567890 you need to write 0x123457890ULL otherwise your number will be truncated to 32 bits and you will get 0x34567890 (the 8 most significant bits don’t fit in 32 bits and are discarded), or, if your compiler is nice, you will get a warning or an error.
Also not that when you pass a floating point number as an argument to a function it always get converted to double precision.
Decimal Encoded Floating Point
There are also floating
point formats that use the decimal system. For our purposes suffices to
know that the digits are 0 through 9, and are
typically encoded using 4b each. One motivation behind these formats is to ensure that
calculations in the base10 system (the one we typically use in our daily life)
are precisely represented. The details of the formats are beyond the scope of
this course. For example, the mantissa is not necessarily
normalized.
Converting from Decimal to Binary
First let’s discuss unsigned integer numbers:
Converting from decimal to binary is done by repeatedly dividing the decimal number by two, writing down the modulo until the result is zero.
The binary representation is the remainders written down in order (that is the remainder of the first division is the most significant bit)
For example, let’s convert 97 to binary:
97 / 2 = 48 and the remainder is 1 (we keep that 1)
48 / 2 = 24 rem. is 0
24/ 2 = 12 rem is 0
12 / 2 = 6 rem. is 0
6 / 2 = 3 rem. is 0
3/ 2 = 1 rem is 1
1 / 2 = 0 rem is 1
Hence the number is 110 0001 in binary and using 7-bits.
If we wanted -97, then we would first convert 97 binary and then take the two’s complement of 97. -97 cannot be represented using 7-bits. This follows from the fact that the MSB in the 7-bit representation 110 0001 is 1. So, we first extend 97 to 8-bits and we get 0110 0001. Now we can take the 2’s complement of that:
2’s complement(0110 0001) = 1001 1111.
Notice that we need an extra bit for the sign.
If we were to write -97 with 16 bits, then we have to sign extend the
representation to 16 bits. This is done by replicating the sign bit as many
times as necessary to reach 16 bits in total as follows:
We start with 8 bits:
1 001 1111
We want a 16-bit number, thus we are missing 8 bits. We replicate the sign bit (the leftmost 1) 8 times:
1111 1111 1001 1111
This is -97 in 16 bits.
If we were to write 97 with 16 bits, we just add as many zero bits as needed to fill in 16 bits:
We start with 7 bits 1100001 and add 9 zero bits:
0000 0000 0110 0001
This is 97 in 16 bits.
Real numbers:
The conversion of real numbers of the form X.Y can be done separately for the integer part X and for the fractional part Y. We covered integer conversion previously. Here we focus on converting the fractional part of numbers of the form 0.Y. This is done by repeatedly multiplying the number by 2. Each time we multiply by 2 a number of the form 0.Y we will get either a number of the form 1.W or 0.W where W some number. The binary representation of the original number is given by the integer part of these multiplications. Each time we multiply by two we keep the integer part aside, and then continue with 0.W. Here’s an example:
Say we want to covert 0.625 to binary.
0.625 x 2 = 1.25 we keep the 1 aside (integer part) and continue with the fractional part (0.25)
0.25 x 2 = 0.5 keep the 0 aside and continue with 0.5
0.5 x 2 = 1.0 keep the 1 aside, we are left with a 0.0, hence we are done.
The representation is 0.101. The first integer part, is the first digit after the dot.
Here’s another example. Let’s convert 0.3
0.3 x 2 = 0.6 à first digit 0, number so far is 0.0
0.6 x 2 = 1.2 à second digit 1, number so far is 0.01
0.2 x 2 = 0.4 à third digit 0, number so far is 0.010
0.4 x 2 = 0.8 à fourth digit 0, number so far is 0.0100
0.8 x 2 = 1.6 à firth digit 1, number so far is 0.01001
0.6 x 2 = 1.2 à sixth digit 1, number so far is 0.010011
Notice that we reached again 0.6 which we already seen in step 2. Hence if we continue this way, the decimal fractional part will never become zero. Hence it is impossible to represent 0.3 in binary using a finite number of digits. With a finite number of digits we can only *approximate* 0.3
Finally, let’s convert 37.64 to binary. Let’s first do the integer part:
37 / 2 = 18 and rem is 1
18 / 2 = 9 and rem is 0
9 / 2 = 4 and rem is 1
4/ 2 = 2 and rem is 0
2/ 2 = 1 and rem is 0
1 / 2 = 0 and rem is 1
Hence 37 is 100101 in binary.
Now, let’s convert 0.64
0.64 x 2 = 1.28 keep the 1 aside
0.28 x 2 = 0.56 keep the 0 aside
0.56 x 2 = 1.12 keep the 1 aside
0.12 x 2 = 0.24 keep the 0
0.24 x 2 = 0.48 keep the 0
0.48 x 2 = 0.96 keep the 0
0.96 x 2 = 1.92 keep the 1
0.92 x 2 = 1.84 keep the 1
0.84 x 2 = 1.68 keep the 1
0.68 x 2 = 1.36 keep the 1
0.36 x 2 = 0.72 keep the 0
0.72 x 2 = 1.44 keep the 1
0.44 x 2 = 0.88 keep the 0
0.88 x 2 = 1.76 keep the 1
0.72 x 2 = 1.52 keep the 1
If you keep calculating at some point you will reach 1.28 again. This means that it is not possible to represent 0.64 with a finite number of binary digits (even though we can represent 64 no problem). In any case the next three digits are 010
So the full number is 100101.1010001111010111111 in a precision of 24 bits. This can be written as
1.00101101000111101011111 x 2^5
Hence it’s IEEE 754 representation would be
S = 0 for a positive number
E – 127 = 5 => E = 132 = 1000 0100
M = 0010 1101 0001 1110 1011 111 (23 bits)
So, the representation is:
0 1000 0100 0010 1101 0001 1110 1011 111