University of Toronto
Department of Electrical and Computer Engineering
 
ECE241F: Digital Systems
 
Hardware Lab #2

Professor Paul Chow and Professor Jonathan Rose

Fall 1996

**** need to get the datasheet for the 74193

The goals of this lab are to understand the operation of JK flip flops, counters, and ring oscillators. These components are used to build an experiment to measure the delay of a gate.

PART I: Ripple Counter

1. Use JK flip-flops (74LS107, negative edge triggered) to build a 3-bit ripple counter with an asynchronous reset input, as shown in Figure 1. The counter outputs are determined by the Q outputs of the flip-flops. How would you modify this circuit so that after Reset goes low, the counter stops at some count N? The counter should stay at this count until the Reset switch is activated again. Build and test this circuit for N = 4. Test the circuit first by clocking it manually. Then connect it to the oscillator provided in your laboratory setup.

   Note: When building this circuit, you will have some unused inputs. What can happen if you leave them floating (unconnected)? What is the solution?

    
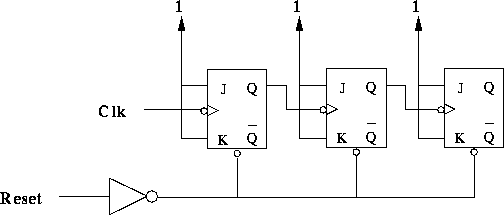
   Figure 1: A 3-bit ripple counter.
   

2. It is required to design a circuit that generates one positive pulse every time a switch is activated. The pulse width should be equal to the width of one clock cycle, as shown in Figure 2. Modify the circuit of Part 1, by choosing a suitable value for N, to obtain the desired pulse.

   Do not disassemble this circuit. You will need it for PART II.

 
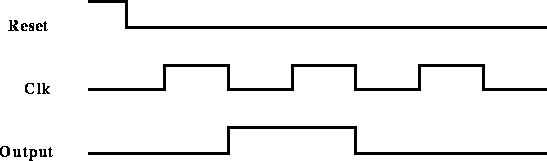
Figure 2: Timing of the desired output.

PART II: Ring Oscillator

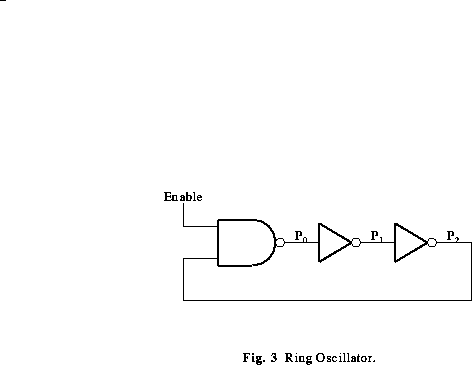
The circuit shown in Figure 3 consists of three inverting gates connected in a ring. While the Enable input is equal to 0, points 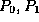, and 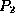will be at logic levels 1, 0 and 1, respectively. Consider what happens when Enable is changed from 0 to 1. The state at point 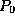is given by:

=

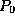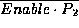
Because of the propagation delay through the gate, the state of 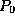at time t is actually a function of the state of the gate inputs at time 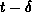, where 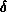is the propagation delay through the gate. That is:

=

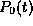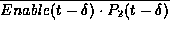
Hence, after one gate delay from the moment Enable becomes equal to 1, 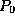becomes equal to 0. One gate delay later, 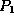changes to 1, and so on. Let 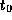be the instant at which Enable changes from 0 to 1. The sequence of events may be described as follows:

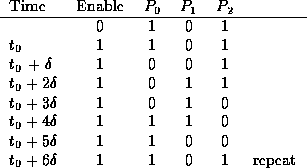
This sequence of events will repeat indefinitely, producing oscillatory signals at 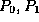, and .

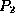1. Draw a timing diagram showing all four signals in Figure 3, starting slightly before ;
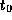2. What is the frequency of oscillation of this circuit?
3. Consider a loop consisting of n gates. Give an expression for the frequency of oscillation as a function of 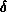and n;
4. What happens when Enable changes back to 0?

The ring oscillator circuit may be used to obtain the gate propagation delay, 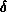, by measuring the oscillator's frequency. Design and build a circuit to do so as follows:

• Set Enable to 1 for a known period of time;
• Count the number of pulses that the oscillator produces during that period.

The required measurements are easily done with the equipment available in the laboratory if you choose n = 13 and a time period equal to one cycle of the built-in oscillator of your setup. Use two 4-bit counter chips (74LS193) to build an 8-bit counter to count the number of pulses. A block diagram for the required circuit is shown in Figure 4 for n = 5.

If you have LogicWorks, you should try to first simulate your circuit. The 74193 is available in the 7400 library. It will help you make sure that you have made the correct connections to the chips. You will have to add some delay to the gates in the ring.

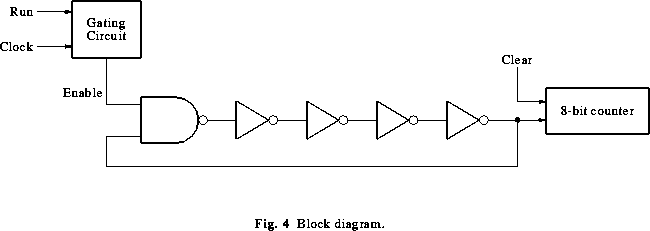
The built-in oscillator has a period of about 20-25 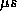when a 10pF timing capacitor is used, but the frequency of oscillation may vary substantially. You must take into account about 20pF of parasitic capacitance for the timing capacitor when using the timing period formula given in the sheet. The parasitic capacitance is due to effects such as the protoboard connections and the wires. This will vary from board to board. Under what conditions will the formula be usable without worrying about the parasitics?

If a logic analyzer is available, you can use it to obtain a more accurate value of the length of the clock cycle. What other ways are there to obtain the clock cycle?

Do your measurement several times and average the results. Why is this a good practice?

Change your circuit by adding a few more inverters, and redo the measurements.

The data sheet for a 74LS04 is included. The delay for a 74LS00 is similar. How do your results compare? If your results disagree, where might the problems lie?