Genetic Algorithm for Transfer Function Design

Introduction

Continuous-time transfer functions for analog filters are often designed using gradient-search techniques such as LMS adaptation. However, for some applications the filter's performance may be a multimodal function of its pole positions. Therefore, the result of a gradient search will, in general, depend upon the optimizer's initial conditions.

The genetic algorithm is a general optimization technique which is intended to find the global minimum of multimodal, multiparameter functions by emulating the process of natural selection. As we shall see, it is well suited to the design of analog filters as long as a relatively fast method for quantifying the filter's performance is available.

The Algorithm

1. Randomly create an initial population of size N. Care should be taken to ensure the initial population does not include many filters which are obviously sub-optimal since the algorithm will waste time evaluating the performance of each.
2. Evaluate the performance function of each filter in the current population.
3. For each filter i in the current population, create n_i copies which will be the "parents" of the next generation. For each filter, n_i is inversely proportional to the performance function of filter i. The result will be a total of M "parents". (M should be greater than N.)
4. Create the next population of filters in the following way:
   1. Randomly choose two parents from the set of M parents.
   2. Create a child by taking the first k filter parameters from parent #1 and the remaining (K-k) filter parameters from parent #2
   3. Repeat steps i-ii. N times resulting in a new population of N filters.
5. "Mutate" each filter in the new population with probability p_mut (usually chosen less than 10%) by adding some random perturbation to each filter parameter.
6. Go back to step 2.

After repeating the procedure for about 10 or fewer generations, take the filter with the smallest performance function, and you are done! Note that in order for this procedure to be fast, you require a fast method for evaluating the perfromance function of all the filters in your population (step 2). Furthermore, although the genetic algorithm is fast at finding nearly optimal filters, doing the final fine-tuning for a very accurate transfer function can take many generations. You may, therefore, want to perform a gradient search using the result of your genetic search as an initial condition.

Example: Design of a Continuous-Time Equalizer

Here I show results which I obtained for the design of a 3rd order continuous-time equalizer for a Lorentizian channel. The performance function used is the total squared error (y(t) - d(t))² where y(t) is the impulse response of the channel & equalizer sampled at the baud rate and d(t) is a delayed delta function. Also note that a 5-tap DFE is assumed to be part of the system, so post-cursor ISI is not included for 5 symbol intervals.

MATLAB was used to evaluate the performance functions of each filter in the population. The animation below shows pole-zero plots of the populations after 1, 3, and 8 generations for a population size of 300. The poles and zeros clearly begin to cluster around their optimal values as the evolution proceeds.

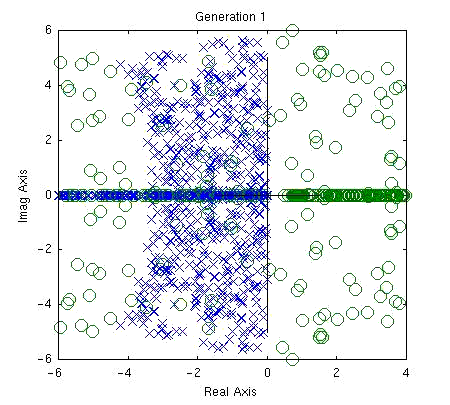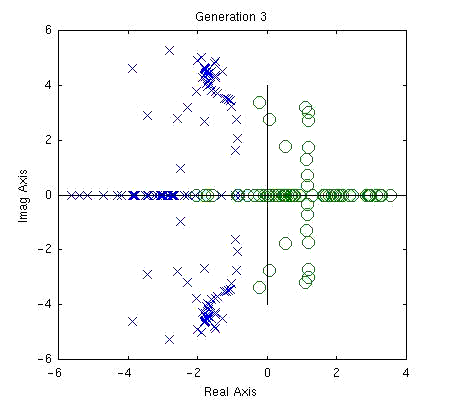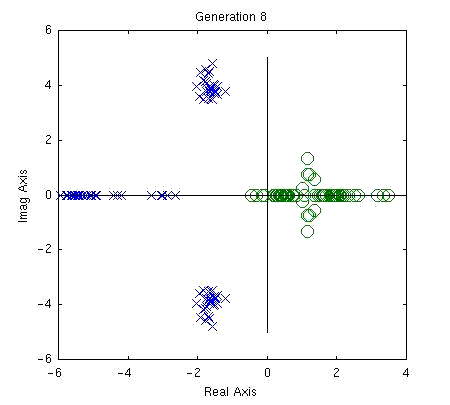
Sample Matlab code for this simulation is available here.

References

B. Widrow and S. D. Stearns, Adaptive Signal Processing, Prentice Hall, New Jersey, 1985, pp. 163-164.

R. Nambiar, C. K. K. Tang and P. Mars, "Genetic and Learning Automata Algorithms for Adaptive Digital Filters," Proc. IEEE Int. Conf. on ASSP, 1992, vol. IV, pp. 41-44.